Présentation de l’exposition Wandlung au

Deutsches Museum et articles de presse

1988

 

Commissaires de l’exposition :

Aspasie Bali et Jeanette Zwingenberger

 

 

 

 

On sait que les nœuds sont présents dans l’environnement humain (la chasse, la pêche…) depuis des millénaires – et aussi, les chaines de la vannerie, du tissage, de la dentelle…

 Depuis un siècle, les mathématiques s’intéressent aux noeuds, essayent de les décrire, de les classifier, de comprendre leur géométrie, de les intégrer à l’espace des Mathématiques.

Cette exposition, constituée d’une suite d’une cinquantaine de modèles tridimensionnels en transformation, a été conçue et réalisée par Jean-François    Chabaud, psychanalyste, élève du Docteur Jacques Lacan, en collaboration avec le Professeur Henri Cartan, co-fondateur de Bourbaki, membre de l’institut de France et de nombreuses Académies étrangères, et notamment l’Académie des Sciences de Bavière.

Cette exposition a été présentée durant dix-huit mois (1986-1988) dans la Salle des Mathématiques du Palais de la découverte, à Paris, qui l’a considérée “comme une première mondiale en matière de diffusion scientifique”.

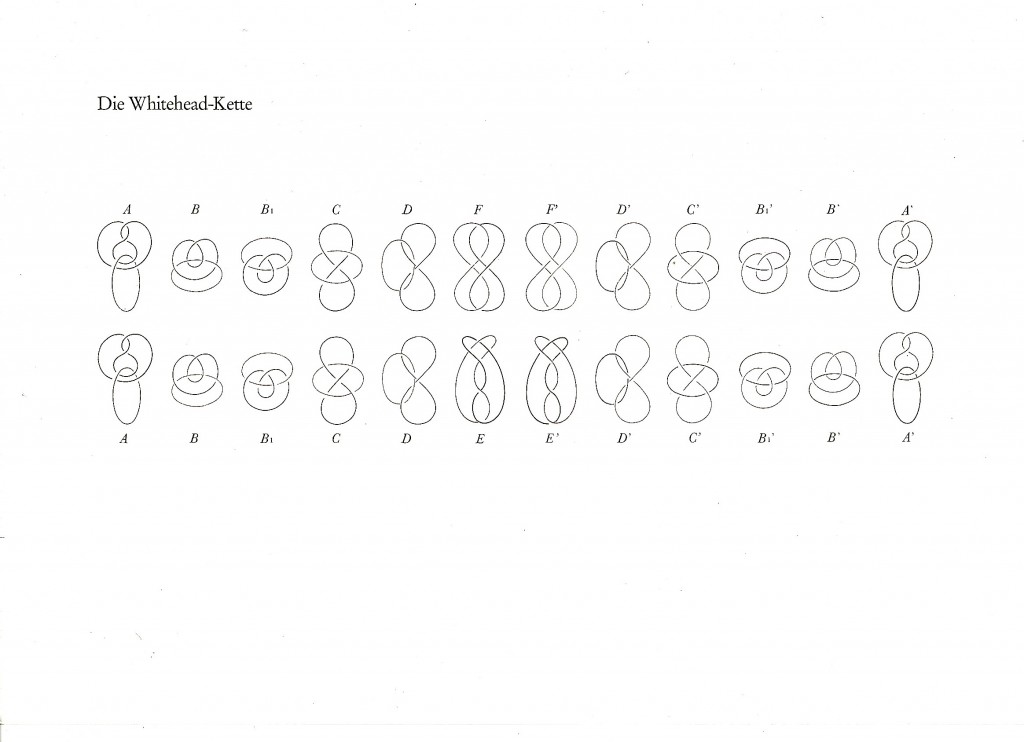
Les auteurs mettent en évidence les transformations successives qui permettent l’interchangeabilité des deux composantes de cette 2-chaîne, nommée par eux dans le champ mathématique “chaîne de J.H.C Whitehead” (en hommage à l’éminent topologue anglais, mort en 1960), et aussi bien, le “nœud dit du fantasme” dans le champ psychanalytique (titre d’un ouvrage de Jean-François Chabaud, en collaboration avec le Professeur Henri Cartan publié en 1984, chez Weber à Bienne, Suisse).

C’est en 1980 que Chabaud s’est intéressé à une suite de dessins nodaux de la chaîne de J.H.C Whitehead, publiée par Jacques Lacan dans son livre XX “Encore” (ed.du Seuil, Paris 1975 ). En effet Jacques Lacan a consacré sa vie à la formalisation de la psychanalyse , ses quelques vingt-cinq dernières années de son oeuvre plus particulièrement à la topologie. L’élaboration psychanalytique de Jacques Lacan en ce qui concerne la topologie appartient à l’extrême interrogation de la psychanalyse. Il nous indique : “L’Analysis situs (nom donné par Leibnitz à ce qui sera, plus tard la topologie) n’est pas à prendre comme il en est des modèles optiques chez Freud au rang de métaphore mais bien pour présenter la structure elle-même” (in “l’Objet de la psychanalyse”) :”un nœud c’est du Réel”.

Dans cette présentation de modèles tridimensionnels, de Jean-François Chabaud et Henri Cartan, s’établit, me semble-t-il une dialectique entre cette suite de nœuds et notre corps, et c’est dire : une mise en jeu de notre corps pris dans sa propre topologie (“l’abîme crie à l’abîme” énonce Angelus Silesius).

Le travail de Chabaud prend appui sur la quatrième figure de cette suite de dessins, proposée, on l’a dit, par Jacques Lacan, dans son séminaire “Encore”. Elle présentifie, avec Lacan, l’écriture topologique du fantasme (soit le mathème $<>(a), mathème qui réunit deux éléments hétérogènes) : la fonction du fantasme étant de réunifier ces deux éléments hétérogènes $ et (a). Dans cette chaîne la boucle présentifie le $, le sujet divisé, et le cercle, l’objet (a), c’est à dire la cause par quoi le sujet s’identifie à son désir.

Dans cette présentation de la topologie mathématique, Jean-François Chabaud et Henri Cartan, mettent en évidence l’interchangeabilité des deux composantes de la chaîne : Chabaud avec sa figure centrale du double huit (1981), et le professeur Henri Cartan avec sa propre trouvaille (1983).

Pour le psychanalyste cette interchangeabilité du double huit est une monstration de la permutation du sujet et de l’objet, soit de la “traversée du fantasme” – la fin de la cure analytique : le passage du psychanalysant au psychanalyste.

Aspasie Bali, 1988

Psychanalyste

 

 

 

 Spektrum (Scientific American) – Article d’Aspasie Bali – 08/1988

 

 

 

 

Article en allemand :

 

 

Article de  Mr Walter  Bauer-Wabnegg  dans Kultur & Technic 04/1988